Introduction
The Challenge of Hemodynamic Assessment in Critical Care
In the high-stakes environment of the Intensive Care Unit (ICU), accurately assessing a patient’s hemodynamic status is paramount. For patients experiencing circulatory shock, rapid and precise diagnosis is the first critical step towards effective treatment [1,2]. Circulatory shock, a life-threatening condition, arises from the body’s failure to deliver adequate oxygen to cells, often manifesting as low blood pressure, tissue hypoperfusion, and elevated lactate levels [3]. It’s a common and grave complication in critical care, affecting approximately one-third of ICU patients and significantly increasing the risk of morbidity and mortality [4].
Diagnosing the underlying cause of hemodynamic instability is far from straightforward. Patients in shock present with a complex interplay of factors, including varying blood volume, cardiac contractility, nervous system activity, vascular tone, and microcirculatory function. Pre-existing health conditions further complicate this already intricate clinical picture [5]. Current methods relying solely on clinical examination to estimate hemodynamic parameters, such as cardiac index, have proven unreliable, often performing no better than random chance [6]. This limitation pushes clinicians towards advanced monitoring technologies to guide treatment decisions [7].
While advanced monitoring is indispensable in complex cases and when initial treatments fail [2,8], over-reliance on technology can overshadow the fundamental importance of clinical examination [9]. Improving the accuracy and reliability of hemodynamic assessments through clinical examination is crucial for optimizing patient care and avoiding the unnecessary escalation to more invasive procedures.
To enhance clinical examination techniques, we must first understand the current diagnostic processes employed by clinicians. Bayesian networks offer a powerful tool to dissect the decision-making behind estimations of cardiac function. By modeling the relationships between clinical findings and diagnostic conclusions, Bayesian networks can illuminate the thought processes that guide clinicians’ assessments of hemodynamic status.
Bayesian networks are increasingly recognized for their utility in medical decision support. Their strength lies in their ability to model complex medical knowledge and uncertainty, representing potential causal relationships between variables [10–13]. These networks integrate prior medical knowledge with data-driven evidence to infer conditional dependencies, providing a framework to analyze clinical reasoning as a step-by-step process where each piece of information is interpreted in light of what is already known [14].
Objectives of the Study
This study leverages Bayesian networks to explore the decision-making process behind cardiac function estimates in ICU patients based on standardized clinical examinations. Our primary goal is to uncover the conditional probabilities that link clinical examination variables to clinicians’ estimations of cardiac function. A secondary objective is to evaluate the diagnostic accuracy of standard clinical examination in estimating cardiac function by comparing these estimations against cardiac index measurements obtained through critical care ultrasonography (CCUS).
Methods
Study Design and Setting
This research is a pre-planned sub-study within the Simple Intensive Care Studies-I (SICS-I) prospective observational cohort study (ClinicalTrials.gov: NCT02912624) [15]. The study received ethical approval from the local institutional review board (METc M15.168207). SICS-I enrolled adult patients admitted to the ICU with an anticipated stay exceeding 24 hours. All participants or their legal representatives provided informed consent. This study adheres to the Standards for the Reporting of Diagnostic Accuracy Studies (STARD) guidelines [16].
Study Aims
The primary aim was to identify the conditional probabilities that link clinical examination findings to the cardiac function estimates made by examiners (students and physicians).
The secondary aim was to assess the diagnostic accuracy of these cardiac function estimates by comparing them to cardiac index values measured using CCUS.
Bayesian Network Analysis Methodology
Bayesian networks are probabilistic graphical models that depict conditional dependencies and independencies between variables using a directed acyclic graph. In these graphs, variables are represented as nodes, and directed edges (arcs) illustrate the conditional dependencies between them. This structure allows the joint probability distribution of all variables to be broken down into simpler, localized probability distributions.
From the initial set of variables collected during clinical examination, we selected 14 relevant clinical variables—derived from bedside monitors, patient records, perfusors, physical examination, and the cardiac function estimate itself—for Bayesian network modeling (see Multimedia Appendix 1). Continuous variables were discretized according to predefined criteria in the study protocol. Correlations between discretized variables were assessed using the Cramér V test.
The network structure was learned using the Max-Min Hill-Climbing algorithm with the Bayesian-Dirichlet equivalent (BDe) scoring metric, implemented in the “bnlearn” R package [17]. This algorithm iteratively refines an initial acyclic graph by adding, deleting, and reversing edges to maximize the BDe score, effectively searching for the network structure that best fits the data [18].
To incorporate prior medical knowledge and ensure network plausibility, we applied constraints by whitelisting (forcing inclusion) and blacklisting (excluding) specific arcs. For instance, arcs directed from other variables to age and gender were blacklisted, as these are not influenced by other clinical variables in the model. Similarly, arcs from estimate to other variables were blacklisted, as the cardiac function estimate does not directly cause changes in the observed clinical variables.
To assess the robustness of the network structure, we employed a bootstrap technique. We generated 2000 bootstrap samples from the original dataset and applied the Max-Min Hill-Climbing algorithm to each. This resulted in 2000 candidate networks, allowing us to calculate a confidence measure for each edge, ranging from 0 (no occurrence in bootstrap samples) to 1 (occurrence in all samples) [13]. We set a minimum significance threshold for arc strength at 0.700 or the calculated significance threshold, whichever was higher, to enhance the robustness of the final consensus network. Edges with a direction coefficient below 0.666 after bootstrapping were considered undirected.
To determine variable distributions and probabilities within the network, we reconstructed the adjacency matrix of the average bootstrapped directed acyclic graph using the Bayesian network function and performed belief propagation using the gRain package [13,19]. Belief propagation enables inference tasks, allowing us to calculate marginal and conditional probabilities. Marginal probability refers to the probability of a variable value occurring across all possible states of other variables, while conditional probability is the probability of a value given specific known values of other variables [20]. These probability queries facilitated the recreation of various clinical scenarios based on the consensus network and the Markov blanket properties. The Markov blanket ensures that when the parent nodes of estimate are known, no other nodes directly influence its conditional distribution [21]. If only some parent nodes are known, ancestors of undefined parent nodes may still indirectly influence the probability of estimate [21].
To validate the network structure beyond bootstrapping, we conducted expert review to assess the physiological plausibility of identified relationships and performed 10-fold cross-validation to evaluate predictive accuracy. The accuracy of cross-validated predictions was assessed by comparing dichotomized estimates (low/high cardiac function) to validated cardiac index measurements and calculating the area under the receiver operating curve (AUC), specificity, and sensitivity.
Definitions and Potential Biases
Patients underwent standardized clinical examination and CCUS according to the SICS-I protocol [15]. The primary variable of interest was the cardiac function estimate made by students or physicians after clinical examination but before CCUS. Examiners categorized cardiac function as “poor,” “moderate,” “reasonable,” or “good.” For diagnostic accuracy analysis and network validation, “poor” and “moderate” estimates were grouped as “low,” while “reasonable” and “good” estimates were grouped as “high.” CCUS image quality and cardiac index measurements were validated by technicians at the Groningen Image Core Lab, blinded to other measurements. Cardiac index was categorized as “low” (≤2.2 L/min/m²) or “high” (>2.2 L/min/m²) [22]. Only patients with both validated cardiac index measurements and cardiac function estimates were included in the Bayesian network analysis. Patients lacking sufficient CCUS image quality or cardiac index measurements were excluded from diagnostic accuracy analysis.
Statistical Methods
Due to the observational nature of the study, a formal sample size calculation was not performed. Statistical analyses were conducted using STATA 15.0 and R version 3.5.1. Data are presented as mean ± SD for normally distributed variables or median (IQR) for skewed data. Categorical data are presented as proportions. Sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), positive likelihood ratio (LR+), and negative likelihood ratio (LR-) with 95% CIs were calculated for both network predictions and examiners’ estimates. Overall accuracy was expressed as the proportion of correctly classified cardiac index measurements.
Results
Patient Demographics
A total of 1075 patients met the inclusion criteria, with 1073 having available cardiac function estimates and included in the Bayesian network analysis. Of these, 783 (73%) had validated cardiac index measurements and were included in diagnostic accuracy tests. Students included 569 patients (73%), and physicians included 214 (27%).
Descriptive Data
Patient characteristics, stratified by the availability of cardiac index measurements, are summarized in Table 1. Body mass index and SAPS II score showed statistically significant differences between the groups (Table 1).
Table 1. Patient Characteristics
| Variable | No cardiac index measurement (n=292) | Cardiac index measurement (n=783) | Total (N=1075) | P value |
|---|---|---|---|---|
| Age (years), mean (SD) | 62 (14) | 62 (15) | 62 (15) | .75 |
| Male gender, n (%) | 188 (64) | 486 (62) | 674 (63) | .49 |
| Body mass index (kg/m2), mean (SD) | 27.5 (5.4) | 26.7 (5.6) | 26.9 (5.5) | .04 |
| Arterial pressure (mm Hg), mean (SD) | 78 (14) | 79 (14) | 78 (14) | .30 |
| Heart rate (bpma), mean (SD) | 87 (22) | 88 (21) | 88 (21) | .35 |
| Irregular heart rhythm, n (%) | 28 (10) | 88 (11) | 116 (11) | .44 |
| Central venous pressure (mm Hg), median (IQR) | 9 (5, 12) | 9 (5, 13) | 9 (5, 13) | .74 |
| Patients administered noradrenaline, n (%) | 142 (49) | 386 (49) | 528 (49) | .85 |
| Urine output (mL/kg/h), median (IQR) | 0.6 (0.3, 1.2) | 0.7 (0.4, 1.2) | 0.6 (0.4, 1.2) | .22 |
| Respiratory rate (bpm), mean (SD) | 18 (5) | 18 (6) | 18 (6) | .50 |
| Mechanical ventilation, n (%) | 179 (61) | 452 (58) | 631 (59) | .29 |
| Positive end-expiratory pressure (cm H2O), median (IQR) | 7 (5, 8) | 7 (5, 8) | 7 (5, 8) | .41 |
| Central temperature (°C), mean (SD) | 37.0 (0.9) | 36.9 (0.9) | 36.9 (0.9) | .84 |
| Difference between central temperature and temperature of the dorsum of the foot (°C), mean (SD) | 7.7 (3.2) | 7.8 (3.2) | 7.8 (3.2) | .66 |
| Subjective “cold” temperature, n (%) | 109 (37.6) | 289 (37.1) | 398 (37.2) | .88 |
| Capillary refill time | ||||
| Knee (s), median (IQR) | 3.0 (2.0, 4.5) | 3.0 (2.0, 4.5) | 3.0 (2.0, 4.5) | .48 |
| Sternum (s), median (IQR) | 2.8 (2.0, 3.0) | 3.0 (2.0, 3.0) | 3.0 (2.0, 3.0) | .84 |
| Finger (s), median (IQR) | 3.0 (2.0, 4.0) | 2.5 (2.0, 4.0) | 2.5 (2.0, 4.0) | .37 |
| Mottling rate, mean (SD) | .64 | |||
| None | 157 (58.8) | 397 (56.8) | 554 (57.3) | |
| Mild | 24 (9.0) | 79 (11.3) | 103 (10.7) | |
| Moderate | 75 (28.1) | 201 (28.8) | 276 (28.6) | |
| Severe | 11 (4.1) | 22 (3.1) | 33 (3.4) | |
| Hemoglobin (mmol/L), mean (SD) | 6.8 (1.5) | 6.8 (1.4) | 6.8 (1.4) | .90 |
| Lactate (mmol/L) | 1.4 (0.9, 2.4) | 1.4 (0.9, 2.2) | 1.4 (0.9, 2.2) | .79 |
| ICUb length of stay (days) | 3.5 (1.9, 6.9) | 3.1 (1.9, 6.5) | 3.2 (1.9, 6.6) | .29 |
| SAPSc II (points) | 47 (37, 58) | 44 (34, 56) | 45 (35, 57) | .037 |
| APACHEd IV score (points) | 77 (56, 92) | 73 (55, 91) | 74 (56, 92) | .14 |
| 90-day mortality, n (%) | 81 (27.7) | 217 (27.7) | 298 (27.7) | .99 |
| Cardiac function estimate, n (%) | .004 | |||
| Poor | 8 (2.8) | 18 (2.3) | 26 (2.4) | |
| Moderate | 46 (15.9) | 165 (21.1) | 211 (19.7) | |
| Reasonable | 164 (56.6) | 349 (44.6) | 513 (47.8) | |
| Good | 72 (24.8) | 251 (32.1) | 323 (30.1) |
abpm: beats per minute.
bICU: intensive care unit.
cSAPS: Simplified Acute Physiology Score.
dAPACHE: Acute Physiology and Chronic Health Evaluation.
Bayesian Network Analysis Findings
The Bayesian network analysis revealed that cardiac function estimates are directly conditionally dependent on two key clinical variables: noradrenaline administration and the presence of delayed capillary refill time or mottling (dCRT-M) (Table 2).
Table 2. Strength and Direction Coefficients of the Consensus Directed Acyclic Graph
| From | To | Strength | Direction |
|---|---|---|---|
| Age | Irregular rhythm | 0.983 | 1.00 |
| Mechanically ventilated | High respiratory rate | 0.994 | 0.504 |
| Mechanically ventilated | dCRT-Ma | 0.875 | 0.884 |
| Irregular rhythm | Tachycardia | 0.848 | 0.954 |
| Tachycardia | High respiratory rate | 0.999 | 0.931 |
| Tachycardia | Low SBPb | 0.821 | 0.883 |
| Tachycardia | Elevated lactate | 0.832 | 0.821 |
| Low SBP | Low MAPc | 1 | 1 |
| Low DBPd | Low MAP | 1 | 1 |
| Elevated lactate level | Oliguria | 0.728 | 0.803 |
| Elevated lactate level | Noradrenaline administration | 1 | 1 |
| Noradrenaline administration | Mechanically ventilated | 1 | 0.957 |
| Noradrenaline administration | Estimate | 0.999 | 1 |
| dCRT-M | Estimate | 0.876 | 1 |
adCRT-M: delayed capillary refill time or mottling.
bSBP: systolic blood pressure.
cMAP: mean arterial pressure.
dDBP: diastolic blood pressure.
The consensus directed acyclic graph (Figure 1) visually represents these relationships. The weakest link in the network, indicated by a dotted line, was the arc from elevated lactate to oliguria (strength coefficient 0.728). The average directionality coefficient was high (0.909), suggesting well-defined directions of influence within the network. Only the edge between mechanical ventilation and high respiratory rate was undirected. Importantly, network structures were consistent across analyses including all participants, students only, or physicians only.
Figure 1. Consensus Directed Acyclic Graph
Probability queries, visualized in a tree diagram (Figure 2), illustrate the conditional probabilities for cardiac function estimate across different clinical scenarios. While tachypnea alone had minimal impact, mechanical ventilation status significantly altered the probability of a “reasonable” or “good” cardiac function estimate (P[ER,G]). Notably, noradrenaline administration consistently lowered P[ER,G], regardless of ventilation status (e.g., P[ER,G|ventilation, noradrenaline]=0.63 vs. P[ER,G|ventilation, no noradrenaline]=0.91). A similar trend was observed for dCRT-M, where the absence of dCRT-M increased the likelihood of a “reasonable” or “good” estimate.
Figure 2. Tree Diagram of Conditional Probability Queries for Cardiac Function Estimate
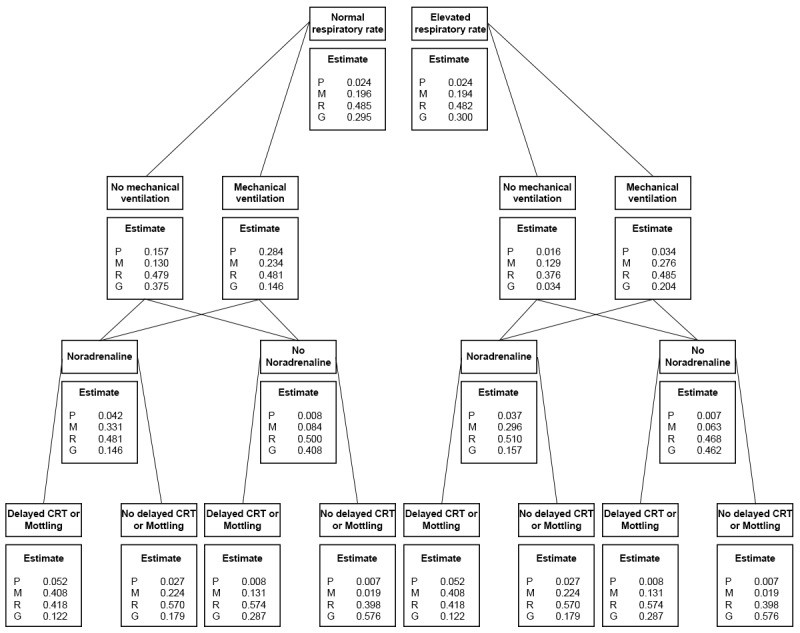 Tree diagram showing the conditional probabilities queries for estimate associated with multiple scenarios during clinical examination. At each step, only the variables above the split are known and as more information becomes available, the conditional probabilities change. P=Poor; M=Moderate; R=Reasonable; G=Good; CRT: capillary refill time.
Tree diagram showing the conditional probabilities queries for estimate associated with multiple scenarios during clinical examination. At each step, only the variables above the split are known and as more information becomes available, the conditional probabilities change. P=Poor; M=Moderate; R=Reasonable; G=Good; CRT: capillary refill time.
The 10-fold cross-validation of the consensus network yielded an AUC of 0.58 for predicting cardiac function, with 79% sensitivity and 36% specificity [23].
Diagnostic Accuracy of Examiners
Diagnostic accuracy for estimating low cardiac index showed sensitivities of 26% (students) and 39% (physicians), and specificities of 83% (students) and 74% (physicians). Positive likelihood ratios were similar for both groups (LR+ = 1.52), while negative likelihood ratios were 0.89 (students) and 0.82 (physicians). Overall accuracy was 63% for students and 61% for physicians (Table 3).
Table 3. Accuracy, Sensitivity, Specificity, Predictive Values, and Likelihood Ratios for Examiners’ Estimates
| Variable | Students (n=569) | Physicians (n=214) | Overall (N=783) |
|---|---|---|---|
| Sensitivity, % (95% CI) | 26 (20-33) | 39 (28-50) | 30 (25-36) |
| Specificity, % (95% CI) | 83 (78-86) | 74 (66-82) | 80 (77-84) |
| Positive predictive value, % (95% CI) | 45 (38-53) | 48 (39-58) | 46 (40-53) |
| Negative predictive value, % (95% CI) | 67 (65-69) | 66 (61-71) | 67 (65-69) |
| Positive likelihood ratio, 95% CI | 1.52 (1.10-2.09) | 1.52 (1.02-2.25) | 1.53 (1.19-1.97) |
| Negative likelihood ratio, 95% CI | 0.89 (0.81-0.98) | 0.82 (0.67-1.00) | 0.87 (0.80-0.95) |
| Overall accuracy, % (95% CI) | 63 (59-67) | 61 (54-67) | 62 (59-66) |
Discussion
Key Observations
Clinical examination remains a cornerstone of initial patient assessment in critical care, offering a readily accessible, cost-effective, and non-invasive method for gathering crucial diagnostic information. Classic clinical signs, such as reduced urine output, altered mental status, and cool, clammy skin, are well-recognized indicators of organ hypoperfusion and are vital in diagnosing circulatory shock [2]. However, the reliability of clinical examination alone in accurately diagnosing low cardiac index has been questioned, with prior research highlighting its limitations [8,9]. Our findings reinforce these concerns, demonstrating persistently low diagnostic accuracy for cardiac function estimates by both students and physicians.
Intriguingly, our Bayesian network analysis pinpointed noradrenaline administration and delayed capillary refill time or mottling as the most influential factors shaping cardiac function estimates. These insights provide a foundation for enhancing the value of clinical examination in two key ways: (1) by identifying potential biases that may lead experienced clinicians to overdiagnose compared to students, and (2) by elucidating the cognitive processes underlying clinical judgment. This deeper understanding can empower clinicians to refine their diagnostic approach, enabling them to consciously evaluate their thinking during clinical examination and prioritize or de-emphasize specific variables in their assessments.
Bayesian Network Analysis: Validation and Limitations
Rigorous validation is essential when employing Bayesian networks to model complex cognitive processes like clinical decision-making. We addressed this challenge through a multi-faceted validation strategy: bootstrapping to generate a robust consensus network, expert review to confirm the physiological plausibility of network relationships, and predictive accuracy assessment [13]. The comparable predictive performance of the Bayesian network to the actual diagnostic accuracy of clinicians strengthens the validity of our network structure as a model of clinical reasoning. It is crucial to reiterate that our objective was not to create a highly optimized predictive model. In fact, if the network had significantly outperformed clinicians in accuracy, it would have been less plausible as a representation of their actual thought processes.
However, this exploratory study has inherent limitations. First, the practical constraints of CCUS applicability meant that cardiac index measurements were not available for all patients, potentially introducing selection bias and contributing to observed differences in SAPS-II score and BMI between patients with and without CCUS data. Second, the necessary discretization of continuous variables for Bayesian network analysis may lead to information loss and potentially alter the true dependency relationships. Finally, deriving causal inferences from Bayesian networks requires the assumption of no unobserved confounding variables. While SICS-I focused on readily available bedside information to mirror the clinical examination setting, limiting the included variables increases the risk of unmeasured confounders. Despite this, the physiological plausibility of the identified dependencies suggests that significant bias may not be present.
Implications for Diagnostic Accuracy: Probability Queries
Previous studies have indicated comparable diagnostic accuracy between experienced physicians and students in estimating cardiac function based on clinical examination [6]. Experienced physicians are known to be more susceptible to cognitive biases, such as confirmation bias and premature closure, compared to students who may maintain a more open and data-driven approach [25,26]. Interestingly, while individual physician accuracy can be modest, diagnostic accuracy improves with group consensus [27]. Our results align with these findings, showing that physicians exhibited higher sensitivity but lower specificity than students, suggesting a tendency towards overdiagnosis, potentially linked to confirmation bias and premature closure.
Further evidence supporting the role of premature closure is the strong influence of noradrenaline and dCRT-M on estimate, suggesting clinicians may overly rely on these readily apparent signs. Probability queries reveal that while mechanical ventilation itself does not directly influence estimate, it significantly alters the probability even before noradrenaline or dCRT-M are considered. This might be because ventilation status is often immediately apparent upon approaching the patient. Furthermore, comparing probability changes based on clinical evidence with likelihood ratios from another SICS-I substudy [15] suggests that earlier indicators like respiratory rate may be underweighted in clinical judgment. For example, despite tachypnea having comparable likelihood ratios to dCRT, the probability queries show a smaller difference in estimated low cardiac function between patients with and without tachypnea compared to those with and without dCRT-M. This indicates a potential cognitive bias towards later, more salient signs like dCRT-M over earlier indicators.
Conclusion and Future Directions
This study reinforces the finding that clinical examination-based cardiac function estimates have limited accuracy for both students and physicians. It highlights noradrenaline administration and delayed CRT or mottling as dominant factors influencing these estimations. While replicating the complex thought processes of clinicians remains challenging, Bayesian networks offer a promising avenue to deconstruct and better understand the educated guessing process in clinical diagnosis. The insights gained, such as the potential over-reliance on certain salient signs and the underutilization of earlier indicators, can inform educational strategies to improve clinical reasoning and variable prioritization during examination. Our team is currently developing an interactive educational game based on SICS-I findings to train medical professionals in cardiac function assessment, utilizing bedside data and Bayesian network-derived insights to enhance diagnostic skills.
Abbreviations
APACHE Acute Physiology and Chronic Health Evaluation
CCUS critical care ultrasonography
DBP diastolic blood pressure
dCRT-M delayed capillary refill time or mottling
ICU intensive care unit
LR- negative likelihood ratios
LR+ positive likelihood ratios
MAP mean arterial pressure
NPV negative predictive values
PPV positive predictive values
SAPS Simplified Acute Physiology Score
SBP systolic blood pressure
SICS-I Simple Intensive Care Studies-I
Appendix
Multimedia Appendix 1
Variables included in the Bayesian network and the respective Cramér V similarity measure.
Footnotes
Authors’ Contributions: TK and JCF performed the data analysis and drafted the manuscript, and all other authors reviewed and provided feedback with each draft. All authors approved of the final manuscript.
Conflicts of Interest: None declared.
References
[References]
Associated Data
Supplementary Materials
Multimedia Appendix 1
Variables included in the Bayesian network and the respective Cramér V similarity measure.